O Teorema de Eudoxo e Algoritmo da Divisão

O clássico Teorema de Eudoxo diz: dados a e b inteiros com b <> 0 então a é um múltiplo de b ou se encontra

Ou seja, existe um inteiro q tal que:

q*b <= a <= (q +1)*b, para b>0.

O teorema de Eudoxo segue a mesma lógica das pedrinhas já mostrada anteriormente.

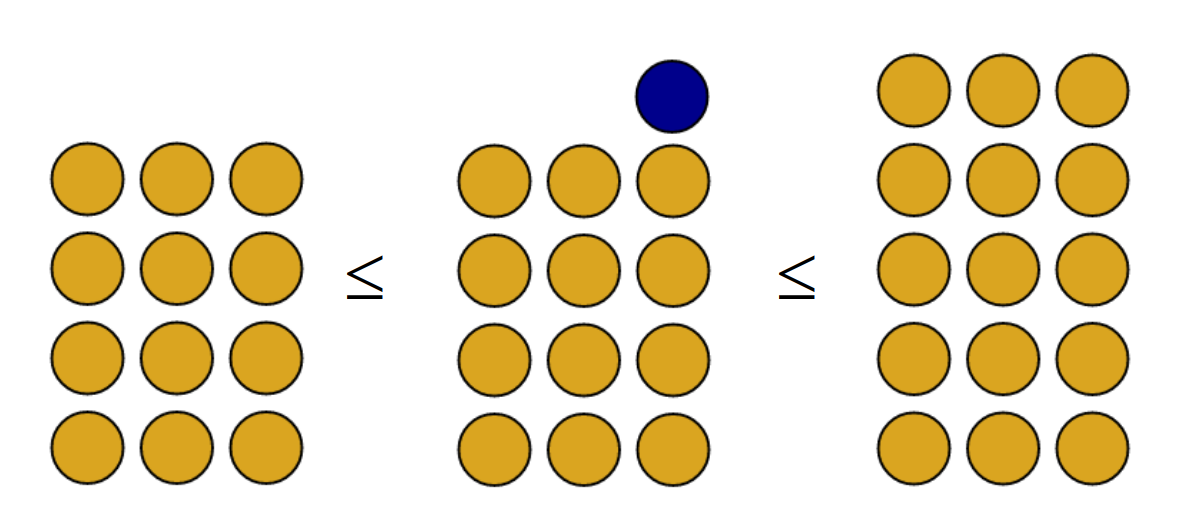
No caso a = 13 e b =3, as pedrinhas vão estar dispostas em 3 colunas, com uma pedrinha de resto.

Existe q = 4 tal que q*b = 12 menor do que 13 (basta tirar a linha do resto), e (q+1)*b = 15, maior do que 13

O Teorema de Eudoxo não é muito famoso, porém, ele é base para mostrar o bem mais interessante Algoritmo

O Algoritmo da Divisão

Dados a e b inteiros com b <> 0, existe um inteiro q e um resto r tal que:

a = q*b + r, com 0 <= r

A visualização é exatamente a mesma, é como pegar a bolinhas e ir distribuindo em b colunas. Ou as últimas pedrinhas vão completar exatamente todas as colunas ou vai sobrar um resto, que vai cobrir apenas algumas colunas.

O livro de referência abaixo divide a prova mais formal em existência e unicidade. A parte de existência parte do Teorema de Eudoxo, dado acima. A de unicidade, começa assumindo que há duas soluções, e a seguir, mostrar que são iguais.

Para uma prova mais formal, vide referência abaixo.

Referência: Introdução à Teoria dos Números, José Plínio de Oliveira Santos, Instituto Nacional de Matemática Pura e Aplicada.

Veja também:

Forgotten Math

Forgotten Lore - Ideias Técnicas com uma pitada de filosofia.