Mais visualizações via “álgebra de pedrinhas” para ajudar a explicar a Teoria dos Números.
1 | n
Basta imaginar que n bolinhas podem ficar em uma coluna, independente do tamanho de n.

d | n -> a * d | a * n, com a inteiro
Digamos que n = 6 e d = 3,
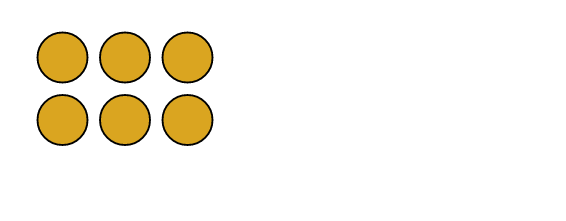
Visualizando, é como copiar e colar esse bloco todo, a vezes, para a direita. Como d | n, não há bolinhas “sobrando”, e não haverá bolinhas sobrando, ao replicar o bloco a vezes.
Ex. n = 6, d = 3 e a = 2

a * d | a * n e a <> 0 -> d | n
Esse aqui é exatamente o inverso do anterior.
Ex. 6 | 18 pode ser representado no diagrama abaixo.
Mas é a mesma coisa que 3*2 | 3 * 6, ou seja, a = 3, d = 2 e n = 6.
Pintei os a = 3 bloquinhos de d = 2 e n = 6 de cores diferentes, para visualização.

d | n e n <> 0 -> |d| <= |n|
Novamente, é útil pensar em pedrinhas colocadas em colunas.
Se d | n, e n <> 0, consigo colocar as n bolinhas em d colunas. Representando as fronteiras das d colunas como linhas, no diagrama abaixo.
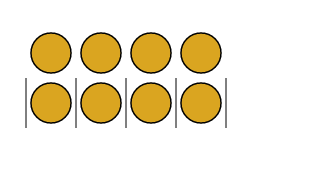
Já se n < d, digamos n = 4 e d = 5, sempre vai “sobrar” uma ou mais casas vazias, de modo que não consigo preencher as todas colunas – e, portanto, d não divide n.

d | n e n | d -> |d| = |n|
Essa afirmação é consequência do teorema acima. Se d | n, d <= n, por outro lado, se n | d, n <= d, e isso só é possível se |d| = |n| (em módulo porque os números podem ser negativos).
Exercício. Se eu tenho 13 pombos e 6 casas para comportá-los, mostre que pelo menos uma casa terá 3 pombos.
Resolução: pela visualização em álgebra de pedrinhas, fica evidente que consigo distribuir igualmente 12 pombos em 6 casas, duas de cada. Porém, ainda tem um pombo restante, de modo que uma casa terá pelo menos 3 pombos.
Esse é o “Princípio da Casa dos Pombos”.

Continue acompanhando a série “Teoria dos Números Visual”.
Veja também:
Forgotten Lore - Ideias Técnicas com uma pitada de filosofia.