Quadrados mágicos são números arranjados numa grade, de tal forma que a soma das linhas, colunas e diagonais seja igual.
A questão de como criar diversos tipos de quadrados mágicos vem intrigado os matemáticos há séculos.

Veremos neste tutorial, como criar um quadrado mágico de qualquer tamanho. Implementação em VBA e em Python disponível no Github.
Há três casos diferentes:
– quadrados mágicos ímpares,
– do tipo 4*n
– do tipo 4*n+2
Para cada caso, há um algoritmo diferente.
São os que têm número de lado ímpar (3, 5, 7, etc).
Começar colocando o 1 na célula superior do meio. Andar uma casa para a esquerda e uma para cima, para colocar o próximo número. Como o tabuleiro acaba, é como se ele desse a volta e colocasse o número no canto inferior.

Ir repetindo o passo acima, do número 2 para o 3.

Quando a casa em questão já estiver ocupada, como no caso abaixo,

… colocar o próximo número imediatamente abaixo da casa de referência.

Isso é suficiente para gerar qualquer quadrado mágico ímpar.
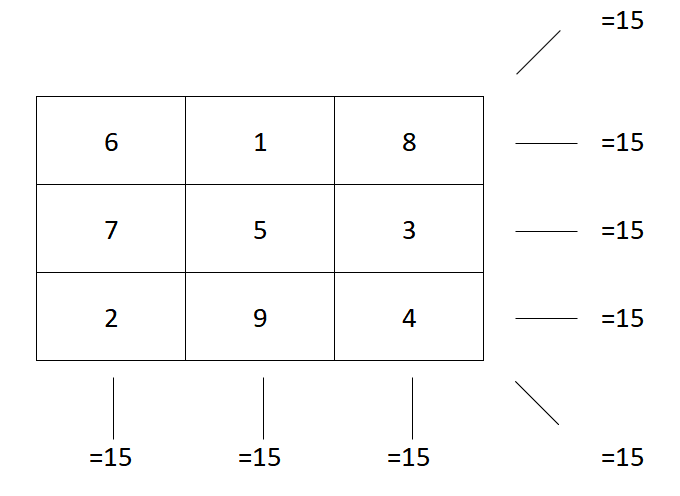
Ex. quadrado mágico 3×3:
Obs. Devido à simetria, tanto faz ir para a direita ou para a esquerda, no primeiro passo acima.

Padrão de cores: mais claro -> número maior, mais escuro, número menor.
Ex. Quadrado mágico 15×15:

Ou seja, quadrados de lado 4, 8, 12, 16, etc.
Colocar os números de 1 a 16 sequencialmente na grade.

Apagar os números da diagonal principal e da diagonal secundária:

Agora, imagine o grid preenchido sequencialmente, mas na ordem inversa:

Neste grid inverso, apagar todos os números que NÃO são das diagonais principal e secundária.

Juntar ambos os quadrados semi-preenchidos, e voilá, temos um quadrado mágico!

Para ordem 8, 12, é similar. É só imaginar um quadrado 8×8 sendo dividido em 4 quadrados 4×4, e para cada quadrado 4×4, aplicar o padrão acima.

São quadrados com casas 6, 10, 14, etc, em que os algoritmos acima não funcionam.
Este caso é mais complicado.
A regra utilizada aqui é a LUX, desenvolvida por John Conway (o mesmo do Jogo da Vida).
Dividir o quadrado em grupos de quadrados 2×2.
Exemplo, um quadrado 6×6 pode ser visto como um grupo de 3×3 quadrados 2×2.
Para o grupo de quadrados, dividir assim:
Até a metade de linhas L
1 linha de U
O restante de X
No exemplo de lado 6, não “cabe” a linha X, mas para casos maiores, sim.

Depois, inverter o L central com o U abaixo:

Note que o grupo de quadrados torna-se um quadrado de ordem ímpar (o primeiro algoritmo descrito).
L, U e X referem-se à padrões de preenchimento:

Portanto, o algoritmo é:
– A ordem de preenchimento é como no caso ímpar, para grupos de quadrados 2×2
– Dentro do quadrado 2×2, usar a regra LUX correspondente ao quadrado.
Exemplo: cubo 6×6

No exemplo acima, começo com 1 no meio na linha superior, que é padrão L:

O próximo número é 5, e o local dele é à direita e acima, conforme o algoritmo de lado ímpar. Esta casa corresponde ao padrão U.

O próximo número é o 9, à direita e acima. Agora, é o padrão L.

E assim sucessivamente.
Ex. Quadrado 10×10.

Utilizando os três algoritmos acima, é possível criar quadrados mágicos de qualquer tamanho, digamos 1000 x 1000.
Implementação em D3: https://asgunzi.github.io/QuadradoMagicoD3/index.html
Implementação em VBA e em Python disponível no Github.
Links:
https://en.wikipedia.org/wiki/Conway%27s_LUX_method_for_magic_squares
https://en.wikipedia.org/wiki/Siamese_method
https://ideiasesquecidas.com/laboratorio-de-matematica/
https://ideiasesquecidas.com/2016/03/09/quadrados-magicos-impares/
Veja também:
Forgotten Lore - Ideias Técnicas com uma pitada de filosofia.